卷积神经网络

写在前面

卷积神经网络来源于图像处理，计算机视觉中要面临一个挑战，就是数据的输入可能会非常大。因为图像是像素点，且彩色图片有3个RGB通道。如果直接使用全连接网络的话，会导致参数数量巨大。在参数如此大量的情况下，难以获得足够的数据来防止神经网络发生过拟合（参数越多，拟合能力越强）和竞争需求，而且这么多的参数需要的内存也让人接受不了。

卷积运算

卷积运算是卷积神经网络最基本的组成部分。
用一个例子来讲，下图是一个6x6的灰度图像，是一个6x6x1的矩阵。为了检测图像中的垂直边缘，可以构造一个3x3的矩阵，称为过滤器或者卷积核。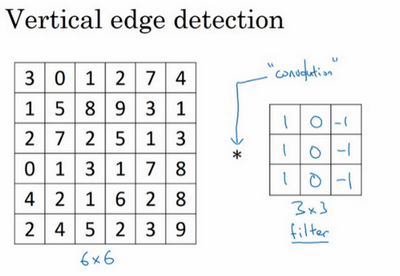
卷积例子

卷积运算就是用卷积核在图像上进行滑动，然后进行元素乘法(element-wise products)，每次将得到的值进行相加。

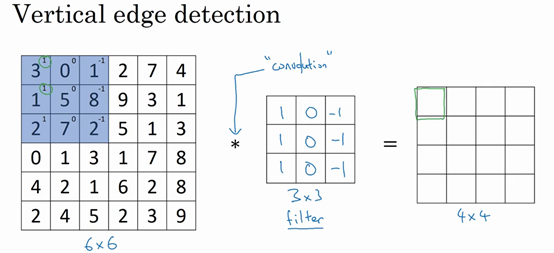
比如我们要计算第一个值，那么进行元素乘法并相加为：

$3\times 1 + 1\times 1 + 2\times 1 + 0\times 0 + 5\times 0 + 7\times 0 + 1\times (-1) + 8\times (-1) + 2\times (-1) = -5$

所以得到的右边矩阵的第一个值就为-5，计算完第一个将卷积核向右移动一格，计算第二个值，在第一行计算完后，向下移动一格，计算第二行的值，直到全部计算完毕，得到下面的值：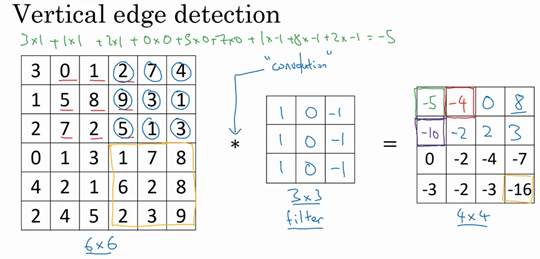
计算结果

左边矩阵是一张图片，中间这个被理解为卷积核，右边的图片我们可以理解为另一张图片。
在编程语言中实现卷积运算：

tensorflow: tf.nn.conv2d()
keras: Conv2D()

为什么这个可以进行垂直边缘检测呢？看下面这个例子：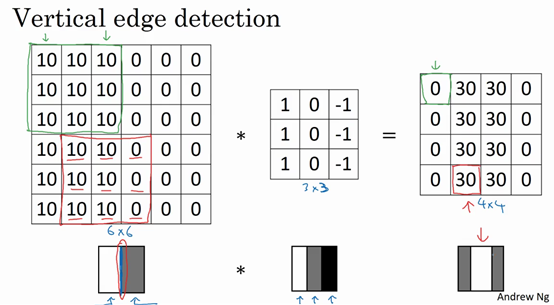

左边这个灰度图像，像素值10是比较亮的像素值，所以左边图像的右边比较暗，左边比较亮，在中间类似有一条垂线。
在经过卷积核卷积运算后，可以看出右边的图像中间要亮些。表示图像中间有一个明显的垂直边缘。

除了可以进行垂直边缘检测的卷积核，还有进行水平边缘检测的卷积核。当然还有许多其他的卷积核。
但是随着深度学习的发展，我们可以把卷积核中的9个数字当成参数，使用反向传播算法去学习这9个参数。这样会学习出很多卷积核，有的可能我们都不知道它的作用，但是在实践中是有效的。

将这9个数字当成参数的思想，已经成为计算机视觉中最为有效的思想之一。

Padding

Padding是卷积的一个基本操作，这是为了构建深度神经网络。
在之前，我们用一个3x3的卷积核去卷积一个6x6的图像，得到是一个4x4的输出。
如果我们有一个nxn的图像，用fxf的卷积核做卷积，那么输出的维度就是(n-f+1)x(n-f+1)。
这样做存在两个缺点:

每次做卷积操作图像就会缩小，可能会缩小到1x1的大小。使得图像的部分信息丢失了。
角落边缘的像素点只被一个输出所触碰或者使用。

为了解决这个问题，我们可以沿着图像边缘再填充一层像素。这样6x6的图像就被填充成一个8x8的图像，这个时候再用3x3的图像对这个8x8的图像卷积，你得到的输出就不是4x4的，而是6x6的图像，这样就和原始图像6x6相同大小。

习惯上，用0去填充，如果p是填充的数量，在这个案例中，p=1，这样输出就变成了(n+2p-f+1)x(n+2p-f+1)，这样来的话输出的图像一样大，而且角落边缘的像素点也不止被一个格子所影响。

当然我们也可以填充两个像素点，即p=2。

选择填充多少像素，通常有两个选择，分别叫做Valid卷积和Same卷积。
Valid卷积意味着不填充，如果你有一个nxn的图像，用一个fxf的卷积核，它将会给你一个(n-f+1)x(n-f+1)维的输出。这就像我们前面的例子似的。
Same卷积意味着填充后，你的输出和输入大小是一样的。根据公式n-f+1，当你填充p个像素点，n就变成了n+2p，最后公式变为n+2p-f+1，因此如果你想让输出和输入大小相等的话，那么即n = n + 2p -f + 1，那么$p = \frac{f-1}{2}$，所以当f是奇数时，只要选择相应的填充尺寸，那么就能确保得到和输入相同尺寸的输出。

习惯上，在计算机视觉中，f通常是奇数。

不使用偶数的原因有两个：

如果f是一个偶数，那么你只能使用一些不对称的填充。只有f是奇数的情况，Same卷积才会有自然的填充。
当你有一个奇数过滤器，比如3x3或者5x5，它就有一个中心点。这样便于指出过滤器的位置。

卷积步长

卷积中的步幅是另一个卷积神经网络的基本操作。

上面的步幅是1，我们也可以把步幅设置成2，即让过滤器每次跳过2个步长。假设步长s = 2，那么输出公式为：$(\frac{n+2p -f}{s} + 1)\times (\frac{n+2p-f}{s} + 1)$。
这个时候有个问题，如果商不是整数怎么办，在这种情况下，我们向下取整。

三维卷积

上面的是对二维图像做卷积，现在我们来对三维图像做卷积。

假设你现在想检测的是彩色图像的特征，彩色图像是6x6x3的，这里的3是3个颜色通道。这时原来的3x3的卷积核要变为3x3x3，卷积核也对应有3层。这时候输出是一个4x4的图像。

三维卷积

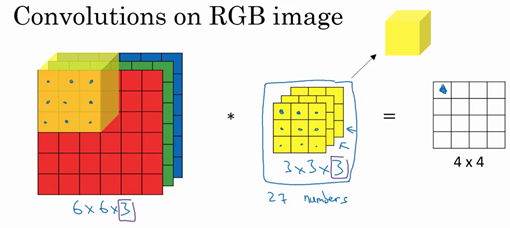
我们可以同时使用多个卷积核（每个卷积核检测不同的特征），这样可以得到的输出维度和卷积核个数有关。比如上面我们使用两个3x3x3的卷积核，那么我们的得到的输出是4x4x2的。
我们用公式来总结一下立体卷积核的维度，假设输入维度是$n\times n\times n{c}$，$n{c}$为通道数目，卷积核大小为$f\times f\times $n{c}$，那么输出就是$ (n-f+1) \times (n-f+1) \times n{k} $，这里的$n_{k}$其实是下一层的通道数，它等于使用的卷积核的个数。这里默认使用的是步幅为1，且未使用padding，如果你使用不同的步幅和Padding，那么n-f+1数值会发生变化，变化方式我们上面已经讲过了。

单层卷积神经网络

对于一层的卷积，首先是运用线性函数在加上偏差，然后应用激活函数ReLU，这样就通过神经网络的一层把一个6x6x3维度转变为一个4x4x2维度的输出。

如果我们将卷积核增加到10个，那么输出就为4x4x10。

我们来计算一下参数，对于一个3x3x3的卷积核，有27个参数，再加上一个偏差，用参数b表示，那么一个卷积核的参数就是28个。如果是10个卷积核的话，参数就是280，和输入图像的维度是没关的。这样我们可以知道参数相对直接应用神经网络来说是很少的，所以这样可以避免过拟合。

总结一下卷积神经网络中的一层（以l层为例）：

单层卷积网络

将上面的单层神经网络堆叠起来，就会构成深度卷积神经网络。

简单神经网络示例

一个典型的卷积神经网络通常有三层，一个是卷积层，常常用Conv来标注，一个是池化层，用POOL来标注，最后一个是全连接层，用FC表示。池化层和全连接层比卷积层更容易设计。
卷积神经网络设计的一个趋势，高度和宽度会在一段时间内保持一致，然后随着网络深度的加深而逐渐减小，而通道数量往往在增加。

卷积网络层类型

虽然仅用卷积层也有可能构建出很好的神经网络，但是大部分情况下还是要添加池化层和全连接层。

池化层

除了卷积层，卷积网络也经常使用池化层来缩减模型的大小，提高计算速度，同时提高所提取特征的鲁棒性。

人们使用最大池化的主要原因是此方法在很多实验中效果都很好。

池化层有一组超参数（f, s），但并没有参数需要学习。上面计算卷积的公式也同样适用于计算池化输出大小：$\frac{n+2p-f}{s} + 1$。
如果输入是3维的，那么输出也是三维的。比如，输入是5x5x2，那么输出是3x3x2，分别对每个通道进行计算。

池化最常用的是最大池化：选取每个过滤器的最大值，还有一种类型的池化，平均池化：选取的不是每个过滤器的最大值，而是平均值。

总结一下，池化的超级参数包括过滤器大小f和步幅s，常用的参数值为f=2，s=2，应用频率非常高。根据公式可以看出效果相当于高度和宽度缩减一半。
超参数padding是很少使用的，最常用的p的值是0.

池化层

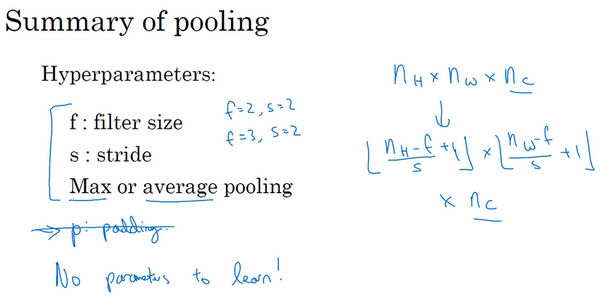
最大池化只是计算神经网络某一层的静态属性，不需要学习。

卷积网络示例

假设我们来实现一个手写数字识别，输入图片大小是32x32x3。
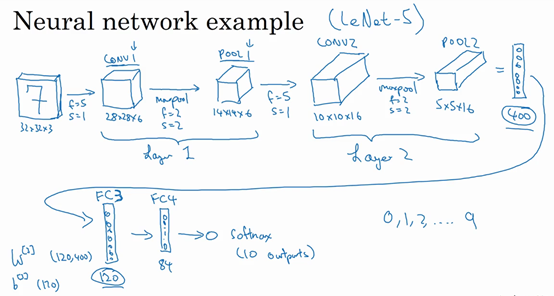
我们构建的网络模型和经典网络LeNet-5非常相似。
第一层使用的过滤器大小为5x5，步幅是1，padding是0，过滤器个数为6。那么输出为28x28x6。将这层标记为CON1，用了6个卷积核，增加了偏差，应用了非线性函数（ReLU）。
然后构建一个池化层，参数f=2， s=2。所以输出为14x14x6。将该层记为POOL1。

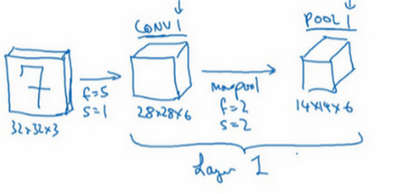
layer1

这儿我们将一个卷积层和一个池化层一起作为一层，比如上面的记为Layer1。

再构建一个卷积层，卷积核大小为5x5，步幅为1，使用16个卷积核，输出为10x10x10的矩阵，标记为CONV2。
然后做最大池化，超参数为f=2, s=2。那么输出结果为5x5x16，标记为POOL2。
上面整体作为神经网络的第二层，即Layer2。

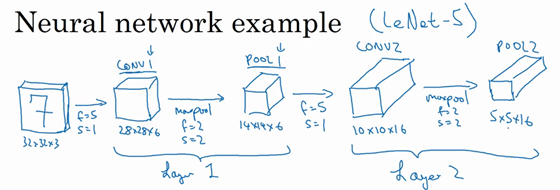
layer2

5x5x16矩阵包含400个元素，将POOL2平整化为一个大小为400的一维向量，利用这400个单元构建下一层，下一层包含120个单元，这就是我们第一个全连接层，标记为FC3。是一个标准的神经网络，维度为120x400。全连接的意思就是这400个单元与这120个单元的每一项连接，还有一个偏差参数。

然后我们在对这120个单元再添加一个全连接层，含有84个单元。标记为FC4。

最后我们用着84个单元填充一个softmax单元，如果我们想识别0-9这10个手写数字，这个softmax就会有10个输出。

arch

这儿我用keras实现了上面的卷积神经网络结构，代码如下

def lenet_5(input_shape=(32, 32, 1), classes=10):
    X_input = Input(input_shape)
    # Layer1
    X = Conv2D(6, (5, 5), strides=(1, 1), padding='valid', name='conv1')(X)
    X = Activation('tanh')(X)
    X = MaxPool2D((2, 2), strides=(2, 2), name='pool1')(X)
    # Layer2
    X = Conv2D(16, (5, 5), strides=(1, 1), padding='valid', name='Conv2')(X)
    X = Activation('tanh')(X)
    X = MaxPool2D((2, 2), strides=(2, 2))(X)
    # FC3
    X = Flatten()(X)
    X = Dense(120, activation='tanh', name='fc3')(X)
    # FC4
    X = Dense(84, activation='tanh', name='fc4')(X)
    # softmax
    X = Dense(classes, activation='softmax')(X)

    model = Model(inputs=X_input, outputs = X, name='lenet_5')
    return model

model = lenet_5(input_shape=(32, 32, 1), classes=10)
adam = optimizers.Adam()
model.compile(optimizer=adam, loss='categorical_crossentropy', metrics=['accuracy'])
model.fit(X_train, Y_train, epochs=3, batch_size=16, verbose=0)

一个卷积神经网络包括卷积层、池化层和全连接层。许多计算机视觉研究正在探索如何把这些基本模块整合起来，构建高效的神经网络，整合这些基本模块需要深入的理解。
找到整合基本构造模块的最好方法就是大量阅读别人的案例。

为什么使用卷积

和只用全连接层相比，卷积层的两个主要优势在于参数共享和稀疏连接。

参数共享：观察发现，特征检测如垂直边缘检测如果适用于图片的某个区域，那么它也可能适用于图片的其他区域。
稀疏连接：在每一层，每个输出值只依赖于很小一部分输入。比如3x3的卷积，只依赖于这个3x3的输入的单元格。

卷积神经网络可以通过这两种机制减少参数，防止过拟合。

卷积神经网络善于捕捉平移不变，通过观察发现，向右移动两个像素，图片中的猫依然清晰可见，因为卷积神经网络的卷积结构使得即使移动几个像素，这张图片依然具有非常相似的特征，应该属于同样的输出标记。