吴恩达序列模型：循环序列模型

发表于 | 更新于 | 分类于 |
本文字数： 4.2k | 阅读时长 ≈ 4 分钟

一些序列的数据：

  • 语音识别
  • 音乐生成
  • 情感分类
  • DNA序列分析
  • 机器翻译
  • 视频动作识别
  • 命名实体识别

数学符号

关于单词的表示，可以构建词汇表，然后通过one-hot进行表示。对于不存在的单词，可以创建一个新的标识来表示。

循环神经网络模型

为什么不使用标准的神经网络？

  • 输入输出在不同的样例中长度不同
  • 不共享从文本不同位置学到的特征
    比如在位置1学到Bob是个人名，我们希望在其他地方出现Bob的时候也能识别是个人名

循环神经网络

循环神经网络引入了隐状态h(hidden state)的概念，h可以对序列形数据提取特征，接着再转换为输出。

隐藏状态

网络结构如下图：
循环网络结构
循环神经网络的限制是在某时刻仅仅只使用了前面时刻的信息，并没有使用后面的信息。

He said, “Teddy Roosevelt was a great President.”
He said, “Teddy bears are on sale!”

对于上面这两个句子，仅仅使用Teddy前面的信息是无法判断Teddy是否是人名。
可以使用双向循环神经网络(BRNN)来解决这个问题。

前向传播

前向传播

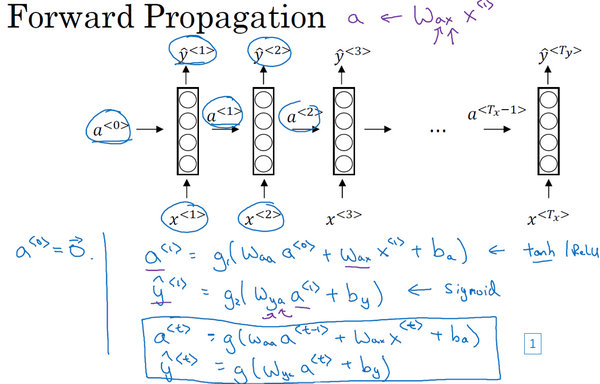
进行符号简化：

符号化简

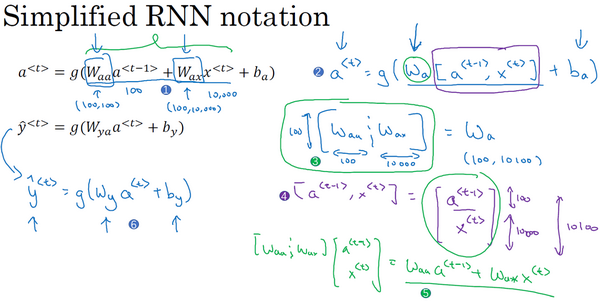
不用使用两个参数矩阵，可以融合成一个参数矩阵。

通过时间的反向传播

计算损失函数：

总体损失

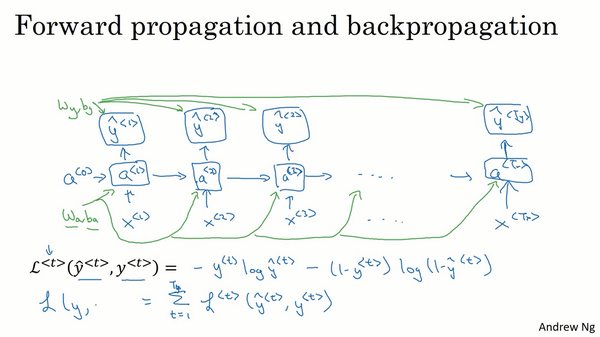
反向传播计算，更新参数

反向传播

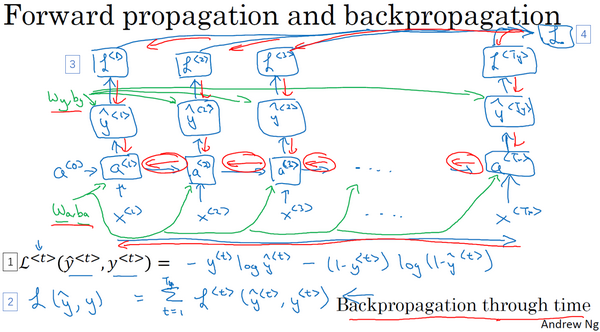
反向计算时，似乎在进行时空穿梭，从现在回到过去，进行梯度计算和参数更新。

不同类型的循环神经网络

根据输入输出序列长度的不同，可以把循环神经网络分成不同的类型。
多对多结构

  • 输入序列长度等于输出序列长度
    命名实体识别
  • 输入序列长度和输出序列长度不等（seq2seq模型，Encoder-Decoder模型）
    机器翻译，事实上这一结构就是在机器领域最先提出的。

多对一结构
输出序列长度为1
情感分类

一对一结构
输入序列长度和输出序列长度都为1，这就是一个标准的小型神经网络

一对多结构
音乐生成
一对多结构

总结
循环神经网络结构总结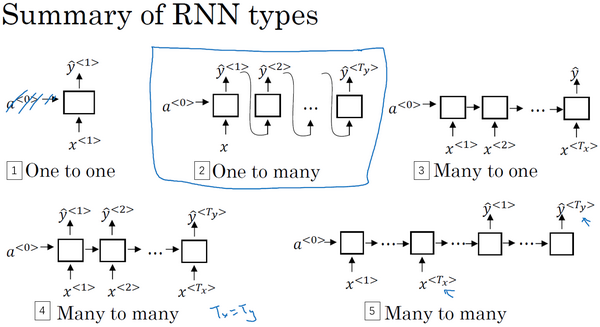

语言模型和序列生成

语言模型
语言模型说得通俗一点就是判断一句话是不是人话。是自然语言中最基础也是最重要的工作之一。

RNN训练语言模型
训练集：大的英文句子语料库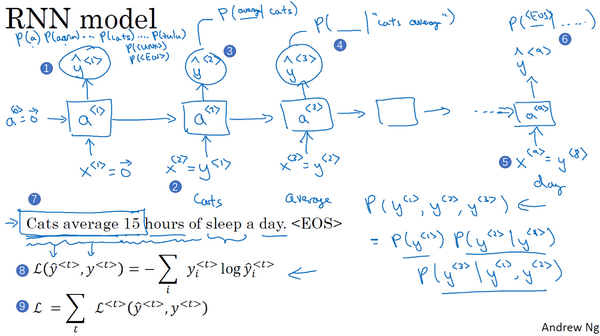
RNN训练语言模型

对新序列采样

在训练一个序列模型之后，要想了解到这个模型学到了什么，一种非正式的方法就是进行一次新序列采样。
一个序列模型模拟了任意特定单词序列的概率，我们要做的就是对这些概率分布进行采样来生成一个新的单词序列。
上面我们都是基于词训练的语言模型，我们也可以在字符级别训练语言模型。
使用字符级别的语言模型生成序列优点：不用担心出现未知字符。但是会得到很长的句子，包含很多字符，且训练起来计算成本比较高昂。

生成模型。

循环神经网络的梯度消失

基本的RNN存在一个很大的问题：梯度消失
对于下面这两个句子，单复数主语和动词前后应该保持一致，即句子中有长期的依赖。

1
2
The cat, which already ate ......, was full.
The cats, which already ate ......, were full.

基本RNN不擅长捕获长期依赖效应。
对于一个很深的网络来说，从输出$\hat{y}$得到的梯度很难传播回去，很难影响靠前层的权重。
RNN同样有这个问题。
所以基本的RNN模型会有很多局部影响。输出的值主要受附近值的影响。
梯度爆炸
随着神经网络层数的增多，梯度不仅可能指数型的下降，也可能指数型的上升。
梯度消失在训练RNN时是首要的问题，尽管梯度爆炸也是会出现。
梯度爆炸很容易发现，参数会大到崩溃，出现NaN。
对于梯度爆炸问题，一个解决方法就是用梯度修剪：观察你的梯度向量，如果大于某个阈值，缩放梯度向量，保证它不会太大。
梯度消失的问题更难解决。

门控循环单元(GRU)

简单GRU

改变了RNN的隐藏层，使其更好的捕捉深层连接，并改善了梯度消失问题。
GRU单元增加了新的变量c，称为记忆细胞(memory cell)。
在时间$t$处，有记忆细胞$c^{< t >}$。对于GRU，$c^{< t >} = a^{< t >}$，但使用不同的标记，但我们说到LSTMs时，这两个会是不同的值。

在每个时间步，我们使用一个候选值重写记忆细胞，即$\tilde{c}^{< t >}$，使用tanh激活函数来计算，

GRU真正核心的思想是有一个门，用$\Gamma _{u}$表示，$u$表示更新门，这是一个0到1之间的值，是使用sigmoid函数得到的。

sigmoid函数总是非常接近0或者非常接近1的，所以$\Gamma _{u}$在大多数情况下非常接近0或1。
使用门决定是否要真的更新$c^{< t >}$。

因为$\Gamma _{u}$很容易接近0，所以$c^{< t >}$几乎等于$c^{< t-1 >}$，即使经过很多步，$c^{< t >}$也很好的被维持，这是缓解梯度消失问题的关键。

完整GRU

对于完整的GRU单元，需要做的改变是增加一个门$\Gamma _{r}$，r可以认为代表相关性(relevance)。下一个$c^{< t >}$的候选值$\tilde c^{< t >}$跟$c^{< t-1 >}$的相关性。

关于为什么要使用现在这个完整版本，而不使用上面那个简单版本，是根据多年来研究者们的实际试验来选择的。完整版本的GRU在很多不同的问题上也是非常健壮和实用的。

你可以尝试发明新版本的单元，只要你愿意，但是GRU是一个标准版本，也是最常使用的。

GRU和LSTM是在神经网络结构中最常用的两个具体实例。

GRU在减少一个门电路的前提下，仍然保持和LSTM近似的性能。

长短期记忆单元(LSTM)

GRU和LSTM对比：

GRU_and_LSTM

可以看到，LSTM没有相关门$\Gamma {r}$，而是增加了遗忘门$\Gamma {f}$和输出门$\Gamma _{o}$，也没有$a^{< t >} = c^{< t >}$。

LSTM

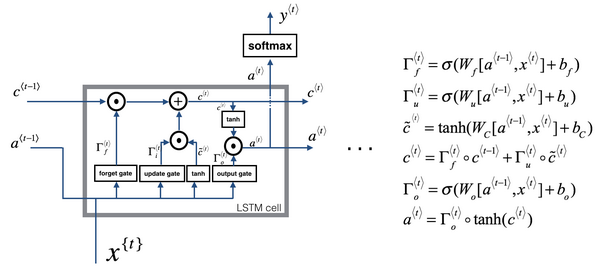
这个LSTM和一般使用的版本会有些不同，最常用的版本可能是门值不仅取决于$a^{< t-1 >}$和$x^{< t >}$，还取决于上一个记忆细胞的值$c^{< t-1 >}$。这称为“偷窥孔连接(peephole connection)”。

对于什么时候用GRU？什么时候使用LSTM？没有统一的准则，LSTM更早出现，而GRU是最近才发明出来的，它可能源于Pavia在更加复杂的LSTM模型中做出的简化。
通常是在任务上尝试这两种模型，看哪种模型的效果更好。

GRU的优点是简单，更容易创建一个更大的网络，而且只有两个门，计算上运行得更快。

LSTM更加强大和灵活，因为它有三个门而不是两个。

LSTM在历史进程上是个更优的选择，可以作为默认的尝试。

双向RNN(Bidirectional RNN)

动机：在上面提到过，命名实体识别中，对某个词的判断关依靠前面的词是不够的，有时还需要依靠后面的词。
对于标准的RNN块、GRU块和LSTM块，只要这些构件都是前向的，则不能解决这个问题。

BRNN

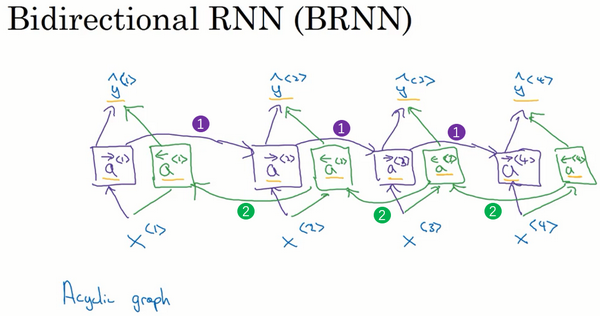
给定一个输入序列$x^{<1>}$到$x^{<4>}$，首先计算前向的$\vec{a}^{<1>}$，然后计算前向的$\vec{a}^{<2>}$，接着$\vec{a}^{<3>}$，$\vec{a}^{<4>}$。
反向序列从计算${\overleftarrow{a}}^{<4>}$开始，反向计算，计算反向的${\overleftarrow{a}}^{<3>}$，最后计算${\overleftarrow{a}}^{<1>}$。
把所有这些激活值计算完了就可以预测结果了。

举个例子，预测结果$\hat y^{< t >}$

对于其中的单元，不仅仅是标准RNN单元，也可以是GRU单元或者LSTM单元。

事实上，很多NLP问题，对于大量有自然语言处理问题的文本，有LSTM单元的双向RNN模型是用得最多的。

双向RNN模型的缺点是需要完整的数据的序列，你才能预测任意位置。

深层循环神经网络(Deep RNNs)

为了学习非常复杂的函数，通常我们会把RNN的多个层堆叠在一起构建更深的模型。

Deep RNN

上面的图就是有3个隐层的新的RNN网络。

比如激活值$a^{[2]<3>}$有两个输入，一个从下面过来的输入，一个从左边过来的输入。

参数$W{2}^{[2]}$和$W{2}^{[2]}$在这一层的计算里都一样，相应的每一层都有自己的参数。
这些单元可以是标准的RNN单元，也可以是GRU单元或者LSTM单元。
标准的神经网络可能会很深，甚至于100层深，而对于RNN来说，有3层就不少了。很少见到堆叠到100层的网络。
但是一种常见的是在每个上面堆叠循环层，但这些层并不水平连接，只是一个深层网络用来预测$y$。

也可以构建深层的双向RNN网络。

从基本的RNN网络，基本的循环单元到GRU，LSTM，再到双向RNN，还有深层版的模型。通过这些可以构建不错的学习序列的模型。

您的支持将鼓励我继续创作！